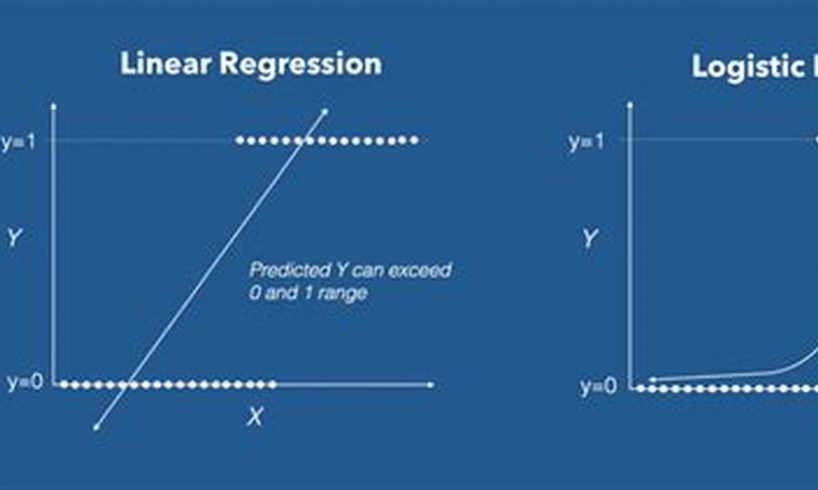
Logistic regression is a statistical model that is used to predict the probability of an event occurring. It is a type of binary classification model, which means that it can be used to predict whether an observation belongs to one of two classes. Logistic regression is often used in situations where the dependent variable is binary, such as predicting whether a patient will recover from a disease or whether a customer will purchase a product.
One of the key assumptions of logistic regression is that the base rate of the event is the same for all observations. This means that the model assumes that the probability of an event occurring is the same for all individuals, regardless of their other characteristics. However, in many cases, this assumption is not true. For example, the probability of recovering from a disease may be different for different patients, depending on their age, sex, and other factors. Logistic regression models can be adapted to recognize these differences by including additional variables that account for the base rate of the event.
There are a number of different ways to incorporate the base rate into a logistic regression model. One common approach is to use a stratified sampling design. This involves dividing the population into different strata, based on their base rate of the event. A separate logistic regression model is then fitted to each stratum. Another approach is to use a covariate adjustment model. This involves adding a variable to the logistic regression model that accounts for the base rate of the event. This variable can be a binary variable that indicates whether the observation belongs to a high-risk or low-risk group, or it can be a continuous variable that measures the individual’s risk of the event.
1. Binary Classification
Binary classification is a type of machine learning task in which the goal is to predict the class of a given input, where the class is one of two possible outcomes. Logistic regression is a statistical model that is often used for binary classification tasks. One of the key features of logistic regression is its ability to recognize different base rates, which is the probability of an event occurring in the absence of any other information.
- Facet 1: How Logistic Regression Recognizes Different Base Rates
Logistic regression recognizes different base rates by using a sigmoid function to model the probability of an event occurring. The sigmoid function is a smooth, S-shaped curve that can take on any value between 0 and 1. The value of the sigmoid function at a given point represents the probability of the event occurring at that point. By using the sigmoid function, logistic regression can model the probability of an event occurring for different values of the input variables, even if the base rate of the event is different for different values of the input variables.
- Facet 2: Examples of Logistic Regression Recognizing Different Base Rates
Logistic regression is used in a variety of applications where the base rate of an event is different for different values of the input variables. For example, logistic regression is used to predict the probability of a patient recovering from a disease, the likelihood of a customer making a purchase, or the probability of a loan being repaid. In each of these cases, the base rate of the event is different for different values of the input variables, such as the patient’s age, sex, and medical history, or the customer’s income, spending habits, and credit score.
- Facet 3: Implications of Logistic Regression Recognizing Different Base Rates
The ability of logistic regression to recognize different base rates is important because it allows the model to make more accurate predictions. For example, in the case of predicting the probability of a patient recovering from a disease, a logistic regression model that recognizes different base rates will be able to make more accurate predictions than a model that assumes that the base rate is the same for all patients. This can lead to better decision-making and improved outcomes for patients.
Overall, the ability of logistic regression to recognize different base rates is a key feature that makes it a powerful tool for binary classification tasks.
2. Stratified sampling
Stratified sampling is a sampling technique that is used to ensure that a sample is representative of the population from which it is drawn. It is often used in situations where the population is divided into different strata, or subgroups, based on a specific characteristic. Logistic regression is a statistical model that is used to predict the probability of an event occurring. One of the key assumptions of logistic regression is that the base rate of the event is the same for all observations. However, in many cases, this assumption is not true. Logistic regression models can be adapted to recognize these differences by using stratified sampling.
By dividing the population into different strata, stratified sampling ensures that the sample is representative of each stratum. This can be important in logistic regression modeling because it allows the model to account for the different base rates of the event in each stratum. For example, if a researcher is interested in predicting the probability of a patient recovering from a disease, they may use stratified sampling to ensure that the sample includes a representative number of patients from different age groups, genders, and racial/ethnic groups. This will allow the logistic regression model to account for the different base rates of the disease in each of these strata.
Stratified sampling is a powerful tool that can be used to improve the accuracy of logistic regression models. By ensuring that the sample is representative of the population from which it is drawn, stratified sampling can help to reduce bias and improve the generalizability of the model. This can be important in a variety of applications, such as predicting the risk of disease, the likelihood of a customer making a purchase, or the probability of a loan being repaid.
3. Covariate Adjustment
Covariate adjustment is a statistical technique that is used to control for the effects of confounding variables in a regression model. Confounding variables are variables that are associated with both the independent and dependent variables in a regression model. If these variables are not controlled for, they can bias the results of the regression model. Logistic regression is a statistical model that is used to predict the probability of an event occurring. One of the key assumptions of logistic regression is that the base rate of the event is the same for all observations. However, in many cases, this assumption is not true. Covariate adjustment can be used to control for the effects of confounding variables and improve the accuracy of logistic regression models.
- Facet 1: How Covariate Adjustment Controls for Confounding Variables
Covariate adjustment controls for the effects of confounding variables by including them as additional variables in the regression model. This allows the model to estimate the effect of the independent variable on the dependent variable, while controlling for the effects of the confounding variables. For example, if a researcher is interested in predicting the probability of a patient recovering from a disease, they may use covariate adjustment to control for the effects of age, sex, and race. These variables are all associated with both the probability of recovering from the disease and the independent variables that are being used to predict the probability of recovery.
- Facet 2: Examples of Covariate Adjustment in Logistic Regression
Covariate adjustment is used in a variety of applications of logistic regression. For example, it is used to predict the probability of a patient recovering from a disease, the likelihood of a customer making a purchase, or the probability of a loan being repaid. In each of these cases, there are a number of confounding variables that can affect the outcome of the event. By using covariate adjustment, researchers can control for the effects of these variables and improve the accuracy of their predictions.
- Facet 3: Implications of Covariate Adjustment for Logistic Regression Models
Covariate adjustment can have a significant impact on the results of logistic regression models. By controlling for the effects of confounding variables, covariate adjustment can reduce bias and improve the accuracy of the model. This can lead to better decision-making and improved outcomes for patients, customers, or other stakeholders.
Overall, covariate adjustment is a powerful tool that can be used to improve the accuracy of logistic regression models. By controlling for the effects of confounding variables, covariate adjustment can help to reduce bias and improve the generalizability of the model. This can be important in a variety of applications, such as predicting the risk of disease, the likelihood of a customer making a purchase, or the probability of a loan being repaid.
4. High-risk group
In the context of logistic regression, a high-risk group is a group of individuals who have a higher probability of experiencing a particular event or outcome compared to the general population. Logistic regression is a statistical model that is used to predict the probability of an event occurring, and it can be used to identify high-risk groups by estimating the probability of an event occurring for different values of the input variables. This information can then be used to develop targeted interventions or strategies to reduce the risk of the event occurring in these high-risk groups.
For example, logistic regression can be used to identify high-risk groups for diseases such as cancer, heart disease, and diabetes. By identifying these high-risk groups, healthcare providers can then focus their efforts on providing preventive care and early intervention to these individuals, which can help to improve their health outcomes. Logistic regression can also be used to identify high-risk groups for financial events, such as loan defaults or bankruptcy. This information can then be used by financial institutions to make more informed lending decisions and to develop targeted financial assistance programs for these high-risk groups.
Overall, the ability of logistic regression to recognize different base rates is a key feature that makes it a powerful tool for identifying high-risk groups. By understanding the different factors that contribute to the risk of an event occurring, logistic regression can help to identify those individuals who are most likely to experience the event and to develop targeted interventions to reduce their risk.
5. Low-risk group
In the context of logistic regression, a low-risk group is a group of individuals who have a lower probability of experiencing a particular event or outcome compared to the general population. Logistic regression is a statistical model that is used to predict the probability of an event occurring, and it can be used to identify low-risk groups by estimating the probability of an event occurring for different values of the input variables. This information can then be used to develop targeted interventions or strategies to further reduce the risk of the event occurring in these low-risk groups.
For example, logistic regression can be used to identify low-risk groups for diseases such as cancer, heart disease, and diabetes. By identifying these low-risk groups, healthcare providers can then focus their efforts on providing preventive care and early intervention to those individuals who are at higher risk, which can help to improve their health outcomes. Logistic regression can also be used to identify low-risk groups for financial events, such as loan defaults or bankruptcy. This information can then be used by financial institutions to make more informed lending decisions and to develop targeted financial assistance programs for those individuals who are at higher risk.
Overall, the ability of logistic regression to recognize different base rates is a key feature that makes it a powerful tool for identifying both high-risk and low-risk groups. By understanding the different factors that contribute to the risk of an event occurring, logistic regression can help to identify those individuals who are most likely to experience the event and those who are least likely to experience the event. This information can then be used to develop targeted interventions to reduce the risk of the event occurring in high-risk groups and to provide preventive care and early intervention to low-risk groups.
6. Risk of event
The risk of an event is the probability that the event will occur. Logistic regression is a statistical model that is used to predict the probability of an event occurring. One of the key features of logistic regression is its ability to recognize different base rates, which is the probability of an event occurring in the absence of any other information.
- Facet 1: How Logistic Regression Recognizes Different Base Rates
Logistic regression recognizes different base rates by using a sigmoid function to model the probability of an event occurring. The sigmoid function is a smooth, S-shaped curve that can take on any value between 0 and 1. The value of the sigmoid function at a given point represents the probability of the event occurring at that point. By using the sigmoid function, logistic regression can model the probability of an event occurring for different values of the input variables, even if the base rate of the event is different for different values of the input variables.
- Facet 2: Examples of Logistic Regression Recognizing Different Base Rates
Logistic regression is used in a variety of applications where the base rate of an event is different for different values of the input variables. For example, logistic regression is used to predict the probability of a patient recovering from a disease, the likelihood of a customer making a purchase, or the probability of a loan being repaid. In each of these cases, the base rate of the event is different for different values of the input variables, such as the patient’s age, sex, and medical history, or the customer’s income, spending habits, and credit score.
- Facet 3: Implications of Logistic Regression Recognizing Different Base Rates
The ability of logistic regression to recognize different base rates is important because it allows the model to make more accurate predictions. For example, in the case of predicting the probability of a patient recovering from a disease, a logistic regression model that recognizes different base rates will be able to make more accurate predictions than a model that assumes that the base rate is the same for all patients. This can lead to better decision-making and improved outcomes for patients.
Overall, the ability of logistic regression to recognize different base rates is a key feature that makes it a powerful tool for predicting the risk of an event. By understanding the different factors that contribute to the risk of an event occurring, logistic regression can help to identify those individuals who are most likely to experience the event and to develop targeted interventions to reduce their risk.
7. Individual characteristics
Individual characteristics play a crucial role in determining the base rate of an event. Logistic regression, a statistical model used to predict the probability of an event occurring, takes into account these characteristics to recognize different base rates. By considering individual characteristics, logistic regression can make more accurate predictions and lead to better decision-making.
- Facet 1: Role of Individual Characteristics in Base Rate Determination
Individual characteristics influence the likelihood of an event occurring. For example, in predicting the probability of a patient recovering from a disease, factors such as age, sex, and medical history can affect the base rate. Logistic regression incorporates these characteristics as input variables to capture their influence on the probability of the event.
- Facet 2: Examples of Individual Characteristics in Logistic Regression
Logistic regression models use various individual characteristics to predict outcomes. In healthcare, patient demographics, lifestyle factors, and genetic information are common characteristics used to estimate the risk of diseases. In finance, credit scores, income, and employment status are used to assess the probability of loan repayment.
- Facet 3: Implications for Logistic Regression Model Accuracy
Considering individual characteristics improves the accuracy of logistic regression models. By tailoring the model to specific characteristics, it can better capture the underlying relationships between variables and the event outcome. This leads to more precise predictions and more effective decision-making.
- Facet 4: Comparison with Models Ignoring Individual Characteristics
Logistic regression models that ignore individual characteristics assume a constant base rate for all individuals. This assumption can lead to biased and inaccurate predictions. By recognizing different base rates, logistic regression provides a more nuanced and realistic representation of the data.
In summary, the consideration of individual characteristics in logistic regression is crucial for recognizing different base rates. By incorporating these characteristics, logistic regression models can make more accurate predictions and improve decision-making across various domains, including healthcare, finance, and marketing.
Frequently Asked Questions on “Does Logistic Regression Recognize Different Base Rates?”
This section addresses common questions and misconceptions about the ability of logistic regression to recognize different base rates.
Question 1: What are base rates?
Answer: Base rates refer to the probability of an event occurring in a given population without considering any specific characteristics or predictors. They represent the overall risk or likelihood of the event in the absence of additional information.
Question 2: Why is it important for logistic regression to recognize different base rates?
Answer: Logistic regression models can make more accurate predictions when they account for different base rates. By recognizing that the probability of an event may vary across different groups or individuals, the model can better capture the underlying relationships and improve its predictive performance.
Question 3: How does logistic regression recognize different base rates?
Answer: Logistic regression uses a sigmoid function to model the probability of an event occurring. This function allows the model to capture non-linear relationships between the input variables and the event outcome. By incorporating relevant variables that represent different characteristics or groups, the model can estimate and adjust for varying base rates.
Question 4: What are some examples of how logistic regression is used to recognize different base rates?
Answer: Logistic regression is widely used in various fields, including healthcare, finance, and marketing. For instance, in healthcare, it can be employed to predict the probability of a patient recovering from a disease, taking into account factors such as age, sex, and medical history. In finance, it can be used to assess the risk of loan default, considering characteristics like credit score, income, and employment status.
Question 5: What are the limitations of logistic regression in recognizing different base rates?
Answer: While logistic regression is capable of recognizing different base rates, it assumes that the relationship between the input variables and the event outcome is linear. In cases where this assumption is violated, alternative modeling techniques may be more appropriate.
Question 6: How can I improve the performance of logistic regression in recognizing different base rates?
Answer: To enhance the performance of logistic regression in recognizing different base rates, it is crucial to carefully select and incorporate relevant variables that represent the underlying characteristics or groups. Additionally, employing techniques such as stratification or covariate adjustment can help control for confounding factors and improve the model’s predictive ability.
Summary: Logistic regression is a powerful tool for recognizing different base rates, leading to more accurate predictions. By considering individual characteristics and group-level factors, it can capture the varying probabilities of events across different populations or subgroups.
Transition to the next section: For further insights into the applications and limitations of logistic regression in recognizing different base rates, please refer to the following section.
Tips for Using Logistic Regression to Recognize Different Base Rates
Incorporating logistic regression into your modeling workflow can provide valuable insights into the relationships between variables and event outcomes. Here are several tips to optimize your use of logistic regression for recognizing different base rates:
Tip 1: Identify Relevant Variables
Carefully select variables that represent the characteristics or groups that may have different base rates. These variables should be relevant to the event being predicted and should have a meaningful relationship with the outcome.
Tip 2: Use Stratification or Covariate Adjustment
Employ techniques like stratification or covariate adjustment to control for confounding factors and reduce bias in your model. This helps ensure that the model accurately captures the varying base rates while accounting for the influence of other variables.
Tip 3: Test for Interactions
Examine whether there are interactions between the variables that represent different base rates and other predictors in the model. Interactions can indicate that the relationship between a predictor and the event outcome depends on the value of another variable.
Tip 4: Evaluate Model Performance
Assess the performance of your logistic regression model using metrics such as accuracy, sensitivity, and specificity. Evaluate the model’s ability to correctly predict events across different base rates and identify potential areas for improvement.
Tip 5: Consider Alternative Modeling Techniques
In cases where the assumption of linearity between predictors and the event outcome is violated, explore alternative modeling techniques such as decision trees or random forests. These methods can handle non-linear relationships and may provide better predictive performance.
Summary: By following these tips, you can effectively utilize logistic regression to recognize different base rates and enhance the accuracy of your predictions. Logistic regression remains a valuable tool for modeling event outcomes, providing insights into the underlying relationships between variables and the likelihood of events occurring.
Transition to the conclusion: To conclude, logistic regression is a powerful tool for recognizing different base rates, enabling more accurate predictions and deeper understanding of data. By carefully considering these tips, you can harness the full potential of logistic regression and make informed decisions in various domains.
Conclusion
Logistic regression is a valuable statistical tool that can recognize different base rates, allowing for more accurate predictions and deeper understanding of data. It is widely used in various fields, including healthcare, finance, and marketing, to model the probability of events occurring. By considering individual characteristics and group-level factors, logistic regression can capture the varying probabilities of events across different populations or subgroups.
To harness the full potential of logistic regression, it is important to carefully select relevant variables, employ techniques like stratification or covariate adjustment, test for interactions, evaluate model performance, and consider alternative modeling techniques when necessary. By following these best practices, practitioners can effectively use logistic regression to gain insights into the relationships between variables and event outcomes, leading to more informed decision-making.
As data becomes increasingly complex and diverse, the ability to recognize different base rates becomes even more crucial for accurate predictions and effective decision-making. Logistic regression remains a powerful tool in this regard, and its continued application will contribute to advancements in various fields.






