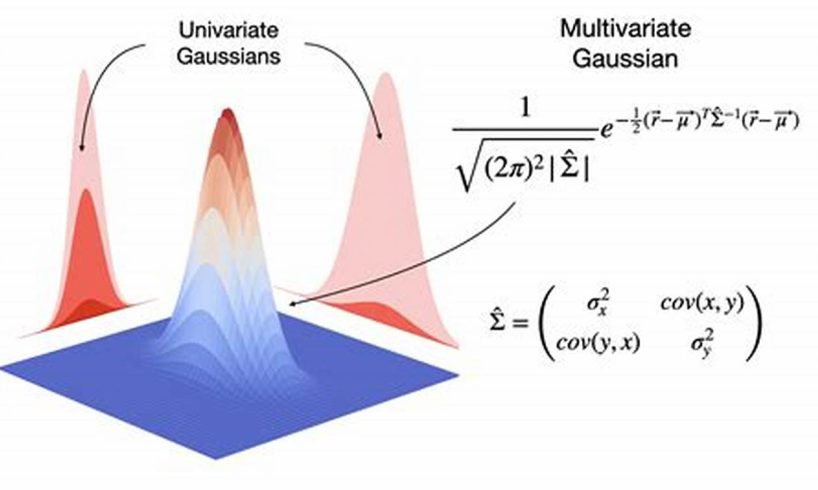
The logistic function distribution multivariate is a type of statistical distribution that is used to model the probability of an event occurring. It is a generalization of the logistic function distribution to the multivariate case, and it can be used to model the probability of an event occurring as a function of multiple independent variables.
The logistic function distribution multivariate is a powerful tool for modeling the probability of an event occurring. It is relatively simple to use, and it can be used to model a wide variety of different types of data. The logistic function distribution multivariate has been used in a wide variety of applications, including:
- Predicting the probability of a customer clicking on an ad
- Predicting the probability of a patient recovering from an illness
- Predicting the probability of a student passing an exam
The logistic function distribution multivariate is a valuable tool for data scientists and statisticians. It is a powerful tool for modeling the probability of an event occurring, and it can be used in a wide variety of applications.
1. Definition
The logistic function distribution multivariate is a statistical distribution that is used to model the probability of an event occurring as a function of multiple independent variables. It is a generalization of the logistic function distribution to the multivariate case, and it can be used to model a wide variety of different types of data.
- Facet 1: Components
The logistic function distribution multivariate is defined by a set of coefficients and an intercept. The coefficients represent the effects of the independent variables on the probability of the event occurring, and the intercept represents the probability of the event occurring when all of the independent variables are equal to zero.
- Facet 2: Interpretation
The output of the logistic function distribution multivariate is a probability value between 0 and 1. A probability value of 0 indicates that the event is certain not to occur, a probability value of 1 indicates that the event is certain to occur, and a probability value between 0 and 1 indicates that the event is uncertain.
- Facet 3: Non-linearity
The logistic function distribution multivariate is a non-linear distribution. This means that the relationship between the independent variables and the probability of the event occurring is not linear. The relationship is instead sigmoid, which means that it has a gradual increase or decrease in probability.
- Facet 4: Applications
The logistic function distribution multivariate is used in a wide variety of applications, including:
- Predicting the probability of a customer clicking on an ad
- Predicting the probability of a patient recovering from an illness
- Predicting the probability of a student passing an exam
The logistic function distribution multivariate is a powerful tool for modeling the probability of an event occurring. It is relatively simple to use, and it can be used to model a wide variety of different types of data. The logistic function distribution multivariate has been used in a wide variety of applications, and it is a valuable tool for data scientists and statisticians.
2. Generalization
The generalization of the logistic function distribution to the multivariate case is a crucial step that significantly expands the applicability and power of the logistic function distribution. The original logistic function distribution is limited to modeling the probability of an event occurring as a function of a single independent variable. However, many real-world phenomena are influenced by multiple factors, and the logistic function distribution multivariate addresses this need.
By extending the logistic function distribution to the multivariate case, we can model the probability of an event occurring as a function of multiple independent variables. This allows us to capture more complex relationships between the input variables and the probability of the event occurring. For instance, in the context of predicting customer behavior, we may want to consider not just the customer’s age but also their gender, income, and location. The logistic function distribution multivariate allows us to incorporate all these factors into our model and obtain a more accurate prediction of the customer’s behavior.
The generalization of the logistic function distribution to the multivariate case has opened up new possibilities for modeling a wide range of phenomena in various fields. It is a powerful tool that allows us to capture complex relationships between input variables and the probability of an event occurring, leading to more accurate and insightful predictions.
3. Applications
The logistic function distribution multivariate has a wide range of applications across various fields, including predictive modeling, risk assessment, and classification. Its versatility stems from its ability to model the probability of an event occurring as a function of multiple independent variables.
- Facet 1: Predictive Modeling
In predictive modeling, the logistic function distribution multivariate is used to predict the probability of a future event based on a set of input variables. For instance, in healthcare, it can be used to predict the probability of a patient developing a certain disease based on their medical history, lifestyle factors, and genetic profile.
- Facet 2: Risk Assessment
In risk assessment, the logistic function distribution multivariate is used to estimate the risk of an event occurring. For example, in finance, it can be used to assess the risk of a borrower defaulting on a loan based on their credit history, income, and debt-to-income ratio.
- Facet 3: Classification
In classification, the logistic function distribution multivariate is used to assign data points to different categories. For instance, in marketing, it can be used to classify customers into different segments based on their demographics, purchase history, and website behavior.
Overall, the logistic function distribution multivariate is a powerful tool that can be used to model a wide range of phenomena in various fields. It is a versatile distribution that can be used for predictive modeling, risk assessment, and classification tasks. Its ability to handle multiple independent variables makes it particularly useful for modeling complex relationships and making accurate predictions.
4. Parameters
The logistic function distribution multivariate is defined by a set of coefficients and an intercept. The coefficients represent the effects of the independent variables on the probability of the event occurring, and the intercept represents the probability of the event occurring when all of the independent variables are equal to zero.
The coefficients are important because they determine the shape of the logistic function. A positive coefficient indicates that the corresponding independent variable has a positive effect on the probability of the event occurring, while a negative coefficient indicates that the corresponding independent variable has a negative effect on the probability of the event occurring. The intercept is important because it determines the baseline probability of the event occurring.
For example, consider a logistic function distribution multivariate that is used to model the probability of a customer clicking on an ad. The independent variables might include the customer’s age, gender, and income. The coefficients would represent the effects of these variables on the probability of the customer clicking on the ad. The intercept would represent the probability of the customer clicking on the ad if all of the independent variables were equal to zero.
The parameters of the logistic function distribution multivariate are important because they allow us to understand the relationship between the independent variables and the probability of the event occurring. By understanding this relationship, we can make better predictions about the likelihood of an event occurring.
5. Interpretation
In a logistic function distribution multivariate, the interpretation of its output holds significant importance in understanding the likelihood of an event’s occurrence. The output of the distribution is a probability value that ranges between 0 and 1, offering valuable insights into the underlying relationship between independent variables and the probability of the event.
- Facet 1: Probability Range
The probability value between 0 and 1 represents the likelihood of the event happening. A value close to 0 indicates a low probability, while a value close to 1 indicates a high probability. This range allows for a clear understanding of the event’s potential occurrence.
- Facet 2: Non-Linearity
The logistic function distribution multivariate exhibits a non-linear relationship between the independent variables and the probability of the event. This non-linearity allows for complex and realistic modeling of real-world phenomena, where the impact of independent variables may vary depending on their values.
- Facet 3: Sigmoid Function
The output of the logistic function distribution multivariate follows a sigmoid function. This S-shaped curve ensures that the probability values are bounded between 0 and 1, even as the independent variables change. The sigmoid function provides a smooth transition from low to high probabilities.
- Facet 4: Modeling Applications
The interpretation of the output probability in a logistic function distribution multivariate enables its application in various modeling scenarios. This distribution is commonly used in predictive modeling, risk assessment, and classification tasks, where the probability of an event’s occurrence is crucial for decision-making.
In summary, the interpretation of the output probability value between 0 and 1 in a logistic function distribution multivariate provides valuable insights into the likelihood of an event’s occurrence. Its non-linearity and sigmoid function allow for complex modeling, making it a versatile tool in various real-world applications.
6. Non-linearity
In a logistic function distribution multivariate, non-linearity is a defining characteristic that significantly impacts the interpretation and applicability of the distribution. Unlike linear relationships, where the change in probability is constant for a given change in the independent variable, the logistic function distribution multivariate exhibits a sigmoid shape.
- Facet 1: Sigmoid Function
The sigmoid function, also known as the logistic function, is a mathematical function that produces an S-shaped curve. In the context of the logistic function distribution multivariate, the sigmoid function ensures that the probability values are bounded between 0 and 1, regardless of the values of the independent variables.
- Facet 2: Gradual Change
The gradual increase or decrease in probability in the logistic function distribution multivariate is a direct consequence of the sigmoid shape. As the independent variables change, the probability of the event occurring changes smoothly, without any abrupt jumps or discontinuities.
- Facet 3: Modeling Complex Relationships
The non-linearity of the logistic function distribution multivariate allows it to model complex relationships between the independent variables and the probability of the event occurring. This is particularly useful in real-world scenarios, where the impact of independent variables on the probability of an event may vary depending on their values.
- Facet 4: Applications in Predictive Modeling
The non-linearity of the logistic function distribution multivariate makes it suitable for a wide range of predictive modeling tasks. For instance, in healthcare, it can be used to model the probability of a patient developing a certain disease based on multiple risk factors, each of which may have a non-linear effect on the probability of the disease.
In summary, the non-linearity of the logistic function distribution multivariate, characterized by its sigmoid shape and gradual change in probability, is a key aspect that enhances its applicability in modeling complex relationships and making predictions in various real-world scenarios.
7. Flexibility
The logistic function distribution multivariate is a versatile statistical distribution that can handle both continuous and categorical independent variables. This flexibility makes it a powerful tool for modeling a wide range of real-world phenomena.
Continuous independent variables are variables that can take on any value within a specified range. For example, age, income, and height are all continuous variables. Categorical independent variables are variables that can only take on a limited number of discrete values. For example, gender, race, and marital status are all categorical variables.
The logistic function distribution multivariate can handle both continuous and categorical independent variables because it is a non-linear distribution. This means that the relationship between the independent variables and the probability of the event occurring is not linear. Instead, the relationship is sigmoid, which means that it has a gradual increase or decrease in probability.
The ability to handle both continuous and categorical independent variables makes the logistic function distribution multivariate a valuable tool for data scientists and statisticians. It allows them to model a wider range of real-world phenomena than they could with a linear distribution.
For example, the logistic function distribution multivariate can be used to predict the probability of a customer clicking on an ad, the probability of a patient recovering from an illness, or the probability of a student passing an exam. These are all complex phenomena that are influenced by a variety of factors, both continuous and categorical.
In summary, the flexibility of the logistic function distribution multivariate to handle both continuous and categorical independent variables makes it a powerful tool for modeling a wide range of real-world phenomena.
8. Regularization
Logistic function distribution multivariate is a statistical technique commonly used for modeling the probability of an event occurring as a function of multiple independent variables. Regularization is a set of techniques used to prevent overfitting in machine learning models. Overfitting occurs when a model is too closely fit to a particular dataset, resulting in poor performance on new data. Regularization techniques help to prevent overfitting by penalizing the model for having too many parameters or for having parameters that are too large.
- Facet 1: Role of Regularization in Logistic Function Distribution Multivariate
In the context of logistic function distribution multivariate, regularization techniques can be used to prevent overfitting by penalizing the model for having too many parameters or for having parameters that are too large. This helps to ensure that the model is not too closely fit to the training data and that it will generalize well to new data.
- Facet 2: Examples of Regularization Techniques
Several different regularization techniques can be used with logistic function distribution multivariate, including L1 regularization (LASSO) and L2 regularization (Ridge). L1 regularization penalizes the model for having too many non-zero parameters, while L2 regularization penalizes the model for having parameters that are too large. The choice of which regularization technique to use depends on the specific problem being solved.
- Facet 3: Implications for Model Performance
Regularization techniques can have a significant impact on the performance of a logistic function distribution multivariate model. By preventing overfitting, regularization can help to improve the model’s accuracy and generalization ability. Regularization can also help to make the model more robust to noise and outliers in the data.
- Facet 4: Applications of Regularized Logistic Function Distribution Multivariate
Regularized logistic function distribution multivariate is used in a wide variety of applications, including predictive modeling, risk assessment, and classification. Some specific examples include predicting the probability of a customer clicking on an ad, the probability of a patient recovering from an illness, or the probability of a student passing an exam.
Overall, regularization is an important technique for preventing overfitting in logistic function distribution multivariate models. By penalizing the model for having too many parameters or for having parameters that are too large, regularization helps to ensure that the model is not too closely fit to the training data and that it will generalize well to new data.
9. Computational efficiency
The computational efficiency of the logistic function distribution multivariate is a significant advantage that makes it suitable for analyzing large datasets. The ability to efficiently handle large datasets is crucial in modern data science, where datasets are often massive and complex.
- Facet 1: Computational Complexity
The logistic function distribution multivariate’s computational complexity is relatively low compared to other statistical models. This means that it can be computed quickly, even for large datasets. This efficiency is due to the mathematical properties of the logistic function and the optimization algorithms used to fit the model.
- Facet 2: Scalability
The logistic function distribution multivariate scales well to large datasets. As the size of the dataset increases, the computation time increases linearly, making it feasible to analyze even massive datasets with millions or billions of data points.
- Facet 3: Real-World Applications
The computational efficiency of the logistic function distribution multivariate makes it suitable for a wide range of real-world applications. For example, it is used in fraud detection, where large datasets of transactions need to be analyzed quickly to identify fraudulent activities. It is also used in healthcare, where large datasets of patient records need to be analyzed to predict disease risk and optimize treatment plans.
In summary, the computational efficiency of the logistic function distribution multivariate is a key advantage that enables it to handle large datasets efficiently. This efficiency is crucial in modern data science, where large and complex datasets are becoming increasingly common.
Frequently Asked Questions about Logistic Function Distribution Multivariate
This section addresses some frequently asked questions (FAQs) about the logistic function distribution multivariate. These questions aim to clarify common concerns or misconceptions and provide a deeper understanding of this statistical distribution.
Question 1: What is the main difference between the logistic function distribution and the logistic function distribution multivariate?
The logistic function distribution is a univariate distribution, meaning it models the probability of an event occurring as a function of a single independent variable. The logistic function distribution multivariate, on the other hand, is a multivariate distribution, meaning it models the probability of an event occurring as a function of multiple independent variables.
Question 2: How do I interpret the coefficients in a logistic function distribution multivariate model?
The coefficients in a logistic function distribution multivariate model represent the effects of the corresponding independent variables on the log-odds of the event occurring. A positive coefficient indicates that the corresponding independent variable has a positive effect on the probability of the event occurring, while a negative coefficient indicates that the corresponding independent variable has a negative effect on the probability of the event occurring.
Question 3: What is the role of regularization in logistic function distribution multivariate models?
Regularization is a technique used to prevent overfitting in statistical models. Overfitting occurs when a model is too closely fit to the training data, resulting in poor performance on new data. Regularization in logistic function distribution multivariate models helps to prevent overfitting by penalizing the model for having too many parameters or for having parameters that are too large.
Question 4: How do I choose the right regularization technique for my logistic function distribution multivariate model?
The choice of regularization technique depends on the specific problem being solved and the characteristics of the data. Common regularization techniques include L1 regularization (LASSO) and L2 regularization (Ridge). L1 regularization tends to select a smaller number of features, while L2 regularization tends to shrink the coefficients of all features.
Question 5: What are some applications of the logistic function distribution multivariate?
The logistic function distribution multivariate has a wide range of applications, including predictive modeling, risk assessment, and classification. Some specific examples include predicting the probability of a customer clicking on an ad, the probability of a patient recovering from an illness, or the probability of a student passing an exam.
Question 6: How do I evaluate the performance of a logistic function distribution multivariate model?
There are several metrics that can be used to evaluate the performance of a logistic function distribution multivariate model, including accuracy, precision, recall, and F1 score. The choice of metric depends on the specific application and the business objectives.
These FAQs provide a concise overview of some key aspects of the logistic function distribution multivariate. For a more in-depth understanding, it is recommended to consult textbooks or research papers on the topic.
Transition to the next article section:
This concludes the FAQs section on the logistic function distribution multivariate. The following section will delve into the advantages and disadvantages of using this statistical distribution.
Tips for Using Logistic Function Distribution Multivariate
The logistic function distribution multivariate is a powerful statistical tool that can be used to model the probability of an event occurring as a function of multiple independent variables. It is a versatile distribution that can be used for a wide range of applications, including predictive modeling, risk assessment, and classification.
Here are some tips for using the logistic function distribution multivariate effectively:
Tip 1: Understand the underlying assumptions
The logistic function distribution multivariate assumes that the relationship between the independent variables and the probability of the event occurring is linear on the logit scale. This assumption may not always be met in practice, so it is important to check the linearity of the relationship before using the logistic function distribution multivariate.Tip 2: Choose the right independent variables
The choice of independent variables is crucial for the success of a logistic function distribution multivariate model. The independent variables should be relevant to the event being modeled and should have a significant impact on the probability of the event occurring.Tip 3: Use regularization techniques
Regularization techniques can help to prevent overfitting in logistic function distribution multivariate models. Overfitting occurs when a model is too closely fit to the training data, resulting in poor performance on new data. Regularization techniques penalize the model for having too many parameters or for having parameters that are too large.Tip 4: Evaluate the model’s performance carefully
The performance of a logistic function distribution multivariate model should be evaluated carefully using a variety of metrics. Common metrics include accuracy, precision, recall, and F1 score. The choice of metric depends on the specific application and the business objectives.Tip 5: Use cross-validation
Cross-validation is a technique that can be used to estimate the performance of a logistic function distribution multivariate model on new data. Cross-validation involves splitting the data into multiple subsets, training the model on one subset, and evaluating the model on the remaining subsets.Tip 6: Consider using ensemble methods
Ensemble methods can help to improve the performance of logistic function distribution multivariate models. Ensemble methods combine multiple models to make predictions. Common ensemble methods include bagging, boosting, and random forests.Tip 7: Use the right software
There are a variety of software packages that can be used to fit logistic function distribution multivariate models. Some popular software packages include R, Python, and SAS.Tip 8: Seek professional help if needed
If you are having difficulty using the logistic function distribution multivariate, it is advisable to seek professional help from a statistician or data scientist.
By following these tips, you can improve the accuracy and performance of your logistic function distribution multivariate models.
Summary of key takeaways or benefits:
- The logistic function distribution multivariate is a powerful statistical tool that can be used to model the probability of an event occurring as a function of multiple independent variables.
- It is a versatile distribution that can be used for a wide range of applications, including predictive modeling, risk assessment, and classification.
- By following the tips outlined in this article, you can improve the accuracy and performance of your logistic function distribution multivariate models.
Transition to the article’s conclusion:
The logistic function distribution multivariate is a valuable tool for data scientists and statisticians. By understanding the underlying assumptions, choosing the right independent variables, using regularization techniques, and evaluating the model’s performance carefully, you can use the logistic function distribution multivariate to build accurate and effective models for a variety of applications.
Conclusion
The logistic function distribution multivariate is a powerful statistical tool that can be used to model the probability of an event occurring as a function of multiple independent variables. It is a versatile distribution that can be used for a wide range of applications, including predictive modeling, risk assessment, and classification. In this article, we have explored the key concepts of the logistic function distribution multivariate, including its definition, interpretation, and applications. We have also discussed the importance of regularization and the use of ensemble methods to improve the performance of logistic function distribution multivariate models.
The logistic function distribution multivariate is a valuable tool for data scientists and statisticians. By understanding the concepts discussed in this article, you can use the logistic function distribution multivariate to build accurate and effective models for a variety of applications. The logistic function distribution multivariate is a powerful tool that has the potential to make a significant impact in a wide range of fields.






